単因子

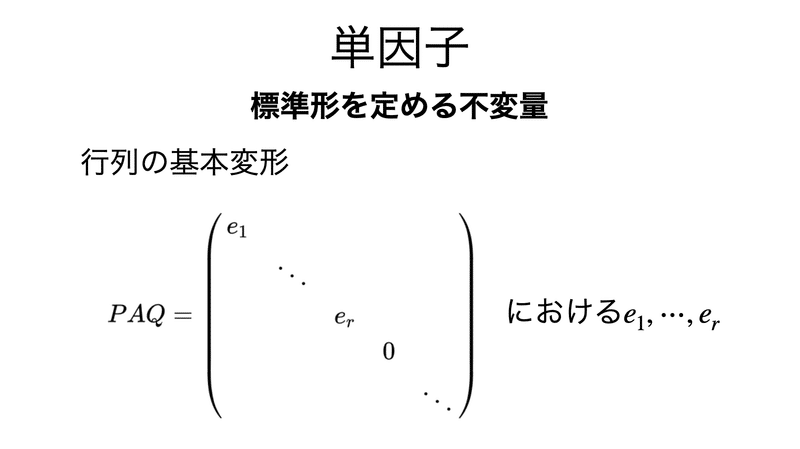
代数学において、行列の単因子（たんいんし）とは、その「標準形」を定める不変量のことである。

定義

D を単項イデアル整域（たとえば整数環 Z や複素係数の一変数多項式環 C[x] などのユークリッド整域）とする。また M_n×m(D) を D 成分の n×m 行列全体とし、特に m = n のときは、これを M_n(D) と表すことにする。すべての行列 A ∈ M_n×m(D) は、ある可逆行列 P ∈ M_n(D) と Q ∈ M_m(D) を使って次の形に変形できる。

PAQ={\begin{pmatrix}e_{1}&&&&\\&\ddots &&&\\&&e_{r}&&\\&&&0&\\&&&&\ddots \end{pmatrix}}

ここで e₁, …, e_r ≠ 0 かつ e₁D ⊇ … ⊇ e_rD である。このような e₁, …, e_r は単数倍を除いて一意に定まり、これを行列 A の単因子という。右辺の行列は A のスミス標準形 Smith normal form あるいは単因子標準形と呼ばれる。この行列 P, Q は行列の基本変形を積み重ねることにより求められる。

性質

F を体とする。

2つの行列 A, B ∈ M_n(F) が相似であるための必要十分条件は、2つの行列 xI − A, xI − B ∈ M_n(F[x]) の単因子が一致することである。

行列 A ∈ M_n(F) の最小多項式は、行列 xI − A ∈ M_n(F[x]) の最大次数の単因子（を規格化したもの）と一致する。

例

D を複素係数の一変数多項式環 C[x] とする。次の行列 A ∈ M₂(C[x]) の単因子は可逆行列 P, Q ∈ M₂(C[x]) として以下の行列を取れば 1, (x − λ)² とわかる。

A={\begin{pmatrix}x-\lambda &-1\\&x-\lambda \end{pmatrix}}

P={\begin{pmatrix}1&\\x-\lambda &1\end{pmatrix}},\qquad Q={\begin{pmatrix}1&\\x-\lambda &1\end{pmatrix}}{\begin{pmatrix}&1\\-1&\end{pmatrix}}

PAQ={\begin{pmatrix}1&\\&(x-\lambda )^{2}\end{pmatrix}}

脚注

参考文献

Hazewinkel, M.; Gubareni, N.; Kirichenko, V. V. (2004). Algebras, Rings and Modules. 1. Kluwer Academic Publishers. ISBN 1-4020-2690-0
Jacobson, Nathan (2009). Basic Algebra I (Second ed.). Dover. ISBN 978-0-486-47189-1. https://books.google.co.jp/books?id=JHFpv0tKiBAC&lpg=PP1&hl=ja&pg=PA181#v=onepage&q&f=false
斎藤正彦『線型代数入門』（初版）東京大学出版会、1966年。ISBN 978-4-13-062001-7。
木村達雄、竹内光弘、宮本雅彦、森田純：「代数の魅力」、数学書房、ISBN 978-4-903342-11-5 (2009年9月10日)　の第2.4節と第2.5節。